Решение систем уравнений методом определителей. Главный определитель системы и определители неизвестных. Теорема Крамера

Лекция 1.1. Числовые матрицы и действия над ними.

Краткое содержание: Место линейной алгебры и аналитической геометрии в естествознании. Роль отечественных ученых в развитии этих наук. Понятие матрицы. Операции над матрицами и их свойства.

Таблица чисел вида называется прямоугольной матрицей размерности . Матрицы обозначаются заглавными латинскими буквами A, B, C, …Числа, из которых состоит таблица, называют элементами матрицы. Каждый элемент имеет два индекса и , обозначающие соответственно номер строки () и номер столбца(), в которых расположен данный элемент. Используются следующие обозначения матрицы .

Две матрицы называются равными , если они имеют одинаковую размерность (т.е. одинаковое число строк и столбцов) и если числа, стоящие на соответствующих местах этих матриц, равны.

Если число строк матрицы равно числу ее столбцов, матрицу называют квадратной . В квадратной матрице число строк (или столбцов) называют порядком матрицы. В частности квадратная матрица первого порядка – это просто действительное число. Соответственно говорят, что вектор строка есть матрица размерности , а вектор-столбец имеет размерность .

Элементы, стоящие на главной диагонали квадратной матрицы (идущей из левого верхнего в правый нижний угол), называются диагональными .

Квадратная матрица все элементы которой не лежащие на главной диагонали равны 0 называется диагональной .

Диагональная матрица, все диагональные элементы которой равны 1, а все внедиагональные – 0, называется единичной и обозначается или , где n- ее порядок.

Основные операции над матрицами – сложение матриц и умножение матрицы на число.

Произведением матрицы А на число называется матрица той же размерности, что и матрица А, каждый элемент которой умножен на это число .

Например: ; .

Свойства операции умножения матрицы на число:

1. l(mА )=(lm)А (ассоциативность)

2. l(А +В )= lА +lВ (дистрибутивность относительно сложения матриц)

3. (l+m)А =)=lА +mА (дистрибутивность относительно сложения чисел)

Линейной комбинацией матриц А и В одинакового размера называется выражение вида: aА +bВ , где a,b - произвольные числа

Суммой матрицА и В (это действие применимо только к матрицам одинаковой размерности) называется матрица С такой же размерности, элементы которой равны суммам соответствующих элементов матриц А и В .

Свойства сложения матриц:

1)А +В =В +А (коммутативность)

2)(А +В )+С =А +(В +С )=А +В +С (ассоциативность)

Разностью матрицА и В (это действие применимо только к матрицам одинаковой размерности) называется матрица С такой же размерности, элементы которой равны разности соответствующих элементов матриц А и В .

Транспонирование . Если элементы каждой строки матрица размерности записать в том же порядке в столбцы новой матрицы, причем номер столбца будет равен номеру строки, то новую матрицу называют транспонированной по отношению к и обозначают . Размерность равна Переход от к называется транспонированием. Ясно так же, что . ,

Умножение матриц . Операция умножения матриц возможна лишь в том случае, если число столбцов первого множителя равны числу строк второго. В результате умножения получим матрицу, число строк которой совпадает с числом строк первого множителя, а число столбцов с числом столбцов второго:

Правило умножения матриц: чтобы получить элемент, стоящий в –й строке и –м столбце произведения двух матриц, нужно элементы –й строки первой матрицы умножить на элементы –го столбца второй матрицы и полученные произведения сложить. На математическом жаргоне иногда говорят: нужно –ую строку матрицы умножить на –й столбец матрицы . Ясно, что строка первой и столбец второй матрицы должны содержать одинаковое количество элементов.

В отличие от этих операций операция умножения матрицы на матрицу определяется более сложно. Пусть заданы две матрицы А и В , причем число столбцов первой из них равно числу строк второй: например, матрица А имеет размерность , а матрица В – размерность . Если

, , то матрица размерности

, где (i=1,…,m;j=1,…,k)

называется произведением матрицы А на матрицу В и обозначается АВ .

Свойства операции умножения матриц:

1. (АВ)С=А(ВС)=АВС (ассоциативность)

2. (А+В)С=АС+ВС (дистрибутивность)

3. А(В+С)=АВ+А (дистрибутивность)

4. Умножение матриц некоммутативно: АВ не равно ВА ., если равно, то эти матрицы называются перестановочными.

Элементарные преобразования над матрицами :

1. Перемена местами двух строк (столбцов)

2. Умножение строки (столбца) на число, отличное от нуля

3. Прибавление к элементам одной строки (столбца) элементов другой строки (столбца), умноженных на какое либо число

Лекция 1.2. Определители с действительными коэффициентами. Нахождение обратной матрицы.

Краткое содержание: Определители и их свойства. Методы вычисления определителей с действительными коэффициентами. Нахождение обратной матрицы дляматриц третьего порядка.

Понятие определителя вводится только для квадратной матрицы. Определитель – это число , которое находится по вполне определенным правилам и обозначается или det A .

Определитель матрицы второго порядка находится так: или

Определителем третьего порядка называется число:

.

Для запоминания этой громоздкой формулы существует «правило треугольников»:

Можно посчитать и другим методом ‑ методом разложения по строке или по столбцу. Введем некоторые определения:

Минором квадратной матрицы А называется определитель матрицы А , который получается вычеркиванием –й строки и –го столбца: например для минор - .

Алгебраическим дополнением элемента определителя называется его минор, взятый со своим знаком, если сумма номеров строки и столбца, в которых расположен элемент, четна, и с обратным знаком, если сумма номеров нечетна: .

Тогда: Определитель третьего порядка равен сумме произведений элементов какого-нибудь столбца (строки) на их алгебраические дополнения.

ПР: Вычислим определитель: , разложив его по элементам первой строки.

Свойства определителей:

1.Определитель равен 0, если содержит две одинаковые строки (столбца) или нулевую строку (столбец).

2.Определитель меняет свой знак при перестановке двух строк (столбцов).

3.Общий множитель в строке (в столбце) можно выносить за знак определителя.

4.Определитель не меняется, если к строке (столбцу) прибавить любую другую строку (другой столбец), умноженную на произвольное число.

5.Определитель не меняется при транспонировании матрицы .

6.Определитель еденичной матрицы равен 1:

7.Определитель произведения матриц равен произведению определителей

Обратная матрица .

Квадратная матрица называется невырожденной , если ее определитель отличен от нуля.

Если при умножении квадратных матриц А и В в любом порядке получается единичная матрица (АВ=ВА=Е ), то матрица В называется обратной матрицей для матрицы А и обозначается , т.е. .

Теорема. Всякая невырожденная матрица имеет обратную .

Алгоритм нахождения обратной матрицы:

Обратная матрица. Квадратная матрица наз невырожденной, если ее определитель отличен от нуля. В противном случае она называется вырожденной.

Матрица, обратная к матрице обозначается . Если обратная матрица существует, то она единственна и

Где – присоединенная (союзная), составленная из алгебраических дополнений j:

Тогда определитель обратной матрицы связан с определителем данной матрицы следующим соотношением: . В самом деле, , откуда и следует данное равенство.

Свойства обратной матрицы:

1. , где ‑ невырожденные квадратные матрицы одинакового порядка.

3. .

4.

Лекция 1.3. Решение систем линейных уравнений методом Крамера.методам Гаусса и средствами матричного исчисления.

Краткое содержание: Метод Крамера и метод Гаусса решения систем линейных алгебраических уравнений. Матричный способ решения систем уравнений. Ранг матрицы. Теорема Кронекера-Капелли. Фундаментальная система решений. Однородные и неоднородные системы.

Система уравнений следующего вида:

(*) , где , ‑ коэффициенты, ‑ переменные, называется системой линейных уравнений. Решить систему линейных уравнений – это значит указать все решения системы, т.е. такие наборы значений переменных, которые обращают уравнения системы в тождества. Система линейных уравнений называется.

Системы линейных уравнений

Система уравнений следующего вида:

где а ij , b i – числовые коэффициенты, x i – переменные, называется системой линейных уравнений.

Решить систему линейных уравнений – значит указать все решения системы, то есть такие наборы значений переменных, которые обращают уравнения системы в тождества.

Система линейных уравнений называется:

совместной, если она имеет хотя бы одно решение;

несовместной, если она не имеет решений;

определенной, если она имеет единственное решение;

однородной, если все b i = 0;

неоднородной, если все b i ≠ 0.

Правило Крамера

(Габриель Крамер (1704-1752) швейцарский математик)

Данный метод применим только в случае систем линейных уравнений, где число переменных совпадает с числом уравнений. Кроме того, необходимо ввести ограничения на коэффициенты системы. Необходимо, чтобы все уравнения были линейно независимы, т.е. ни одно уравнение не являлось бы линейной комбинацией остальных.

Для этого необходимо, чтобы определитель матрицы системы не равнялся 0.

 = det A  0;

Теорема. (Правило Крамера):

Система из n уравнений с n неизвестными

В случае, если определитель матрицы системы не равен нулю, то система имеет единственное решение и это решение находится по формулам:

х i = ;

где  - главный определитель , составленный из числовых коэффициентов при неизвестных, а  i – вспомогательный определитель , получаемый из главного заменой i -го столбца столбцом свободных членов b i .

 i =

Пример. Решить систему, используя правило Крамера.

;

 1 =
;  2 =
;  3 =
;

x 1 = ; x 2 = ; x 3 = ;

Пример. Найти решение системы уравнений:

 =
= 5(4 – 9) + (2 – 12) – (3 – 8) = -25 – 10 + 5 = -30;

 1 =
= (28 – 48) – (42 – 32) = -20 – 10 = -30.

 2 =
= 5(28 – 48) – (16 – 56) = -100 + 40 = -60.

 3 =
= 5(32 – 42) + (16 – 56) = -50 – 40 = -90.

Если система однородна, т.е. b i = 0, то при 0 система имеет единственное нулевое решение x 1 = x 2 = … = x n = 0.

Матричный метод

Матричный метод применим к решению систем уравнений, где число уравнений равно числу неизвестных.

Этот метод удобен для решения систем невысокого порядка. Он основан на применении свойств умножения матриц.

Пусть дана система уравнений:

Введем обозначения:

A =
- матрица коэффициентов системы;

B = матрица – столбец свободных членов;

X = - матрица – столбец неизвестных.

Систему уравнений можно записать в матричной форме:

Сделаем следующее преобразование: A -1 AX = A -1 B,

т.к. А -1 А = Е, то ЕХ = А -1 В, получим

Х = А -1  В - решение матричного уравнения

Пример. Решить систему матричным методом

Решение.Обозначим:

,
,
.

Получаем матричное уравнение
.

Его решение
, т.е.

(Нахождение обратной матрицы было рассмотрено ранее).

Метод Гаусса

(Карл Фридрих Гаусс (1777-1855) немецкий математик)

В отличие от матричного метода и метода Крамера, метод Гаусса может быть применен к системам линейных уравнений с произвольным числом уравнений и неизвестных. Суть метода заключается в последовательном исключении неизвестных.

Рассмотрим систему линейных уравнений:

Определение: Матрица, составленная из коэффициентов при неизвестных системы, называется матрицей системы.

Определение: Матрица называется расширенной матрицей системы, если к матрице А присоединить столбец свободных членов системы.

Расширенная матрица – это закодированная запись системы. Строки матрицы соответствуют уравнениям системы. Умножение уравнения на число и сложение этого произведения с другим уравнением эквивалентно умножению строки матрицы на это число и почленному сложению произведения с другой строкой матрицы. Таким образом, работу с уравнениями можно заменить работой со строками матрицы.

Определение: Матрицу А называют ступенчатой, если:

А) любая ее строка имеет хотя бы один отличный от нуля элемент,

Б) первый отличный от нуля элемент каждой ее строки, начиная со второй, расположен правее неравного нулю элемента предыдущей строки.

Метод Гаусса является эффективным методом решения и исследования систем линейных уравнений. Он состоит в том, что данная система линейных уравнений преобразуется в равносильную ей систему ступенчатого вида, которая легко решается и исследуется. Применение метода Гаусса не зависит ни от числа уравнений, ни от числа неизвестных в системе.

Разберем идею метода Гаусса на конкретных примерах.

Пример. Решить систему линейных уравнений методом Гаусса.

Составим расширенную матрицу системы и с помощью элементарных преобразований приведем к виду:

, откуда получаем: x 3 = 2; x 2 = 5; x 1 = 1.

Пример. Решить систему методом Гаусса.

Составим расширенную матрицу системы.

Таким образом, исходная система может быть представлена в виде:

В ходе решения задач по высшей математике очень часто возникает необходимость вычислить определитель матрицы . Определитель матрицы фигурирует в линейной алгебре, аналитической геометрии, математическом анализе и других разделах высшей математики. Таким образом, без навыка решения определителей просто не обойтись. Также для самопроверки Вы можете бесплатно скачать калькулятор определителей , он сам по себе не научит решать определители, но очень удобен, поскольку всегда выгодно заранее знать правильный ответ!

Я не буду давать строгое математическое определение определителя, и, вообще, буду стараться минимизировать математическую терминологию, большинству читателей легче от этого не станет. Задача данной статьи – научить Вас решать определители второго, третьего и четвертого порядка. Весь материал изложен в простой и доступной форме, и даже полный (пустой) чайник в высшей математике после внимательного изучения материала сможет правильно решать определители.

На практике чаще всего можно встретить определитель второго порядка, например: , и определитель третьего порядка, например: .

Определитель четвертого порядка тоже не антиквариат, и к нему мы подойдём в конце урока.

Надеюсь, всем понятно следующее: Числа внутри определителя живут сами по себе, и ни о каком вычитании речи не идет! Менять местами числа нельзя!

(Как частность, можно осуществлять парные перестановки строк или столбцов определителя со сменой его знака, но часто в этом нет никакой необходимости – см. следующий урок Свойства определителя и понижение его порядка)

Таким образом, если дан какой-либо определитель, то ничего внутри него не трогаем!

Обозначения : Если дана матрица , то ее определитель обозначают . Также очень часто определитель обозначают латинской буквой или греческой .

1) Что значит решить (найти, раскрыть) определитель? Вычислить определитель – это значит НАЙТИ ЧИСЛО. Знаки вопроса в вышерассмотренных примерах – это совершенно обыкновенные числа.

2) Теперь осталось разобраться в том, КАК найти это число? Для этого нужно применить определенные правила, формулы и алгоритмы, о чём сейчас и пойдет речь.

Начнем с определителя «два» на «два» :

ЭТО НУЖНО ЗАПОМНИТЬ, по крайне мере на время изучения высшей математики в ВУЗе.

Сразу рассмотрим пример:

Готово. Самое главное, НЕ ЗАПУТАТЬСЯ В ЗНАКАХ.

Определитель матрицы «три на три» можно раскрыть 8 способами, 2 из них простые и 6 - нормальные.

Начнем с двух простых способов

Аналогично определителю «два на два», определитель «три на три» можно раскрыть с помощью формулы:

Формула длинная и допустить ошибку по невнимательности проще простого. Как избежать досадных промахов? Для этого придуман второй способ вычисления определителя, который фактически совпадает с первым. Называется он способом Саррюса или способом «параллельных полосок».
Суть состоит в том, что справа от определителя приписывают первый и второй столбец и аккуратно карандашом проводят линии:

Множители, находящиеся на «красных» диагоналях входят в формулу со знаком «плюс».
Множители, находящиеся на «синих» диагоналях входят в формулу со знаком минус:

Пример:

Сравните два решения. Нетрудно заметить, что это ОДНО И ТО ЖЕ, просто во втором случае немного переставлены множители формулы, и, самое главное, вероятность допустить ошибку значительно меньше.

Теперь рассмотрим шесть нормальных способов для вычисления определителя

Почему нормальных? Потому что в подавляющем большинстве случаев определители требуется раскрывать именно так.

Как Вы заметили, у определителя «три на три» три столбца и три строки.
Решить определитель можно, раскрыв его по любой строке или по любому столбцу .
Таким образом, получается 6 способов, при этом во всех случаях используется однотипный алгоритм.

Определитель матрицы равен сумме произведений элементов строки (столбца) на соответствующие алгебраические дополнения. Страшно? Все намного проще, будем использовать ненаучный, но понятный подход, доступный даже для человека, далекого от математики.

В следующем примере будем раскрывать определитель по первой строке .
Для этого нам понадобится матрица знаков: . Легко заметить, что знаки расположены в шахматном порядке.

Внимание! Матрица знаков – это мое собственное изобретение. Данное понятие не научное, его не нужно использовать в чистовом оформлении заданий, оно лишь помогает Вам понять алгоритм вычисления определителя.

Сначала я приведу полное решение. Снова берем наш подопытный определитель и проводим вычисления:

И главный вопрос: КАК из определителя «три на три» получить вот это вот:
?

Итак, определитель «три на три» сводится к решению трёх маленьких определителей, или как их еще называют, МИНОРОВ . Термин рекомендую запомнить, тем более, он запоминающийся: минор – маленький.

Коль скоро выбран способ разложения определителя по первой строке , очевидно, что всё вращается вокруг неё:

Элементы обычно рассматривают слева направо (или сверху вниз, если был бы выбран столбец)

Поехали, сначала разбираемся с первым элементом строки, то есть с единицей:

1) Из матрицы знаков выписываем соответствующий знак:

2) Затем записываем сам элемент:

3) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит первый элемент:

Оставшиеся четыре числа и образуют определитель «два на два», который называется МИНОРОМ данного элемента (единицы).

Переходим ко второму элементу строки.

4) Из матрицы знаков выписываем соответствующий знак:

5) Затем записываем второй элемент:

6) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит второй элемент:

Ну и третий элемент первой строки. Никакой оригинальности:

7) Из матрицы знаков выписываем соответствующий знак:

8) Записываем третий элемент:

9) МЫСЛЕННО вычеркиваем строку и столбец, в котором стоит третий элемент:

Оставшиеся четыре числа записываем в маленький определитель.

Остальные действия не представляют трудностей, поскольку определители «два на два» мы считать уже умеем. НЕ ПУТАЕМСЯ В ЗНАКАХ!

Аналогично определитель можно разложить по любой строке или по любому столбцу. Естественно, во всех шести случаях ответ получается одинаковым.

Определитель «четыре на четыре» можно вычислить, используя этот же алгоритм.
При этом матрица знаков у нас увеличится:

В следующем примере я раскрыл определитель по четвертому столбцу :

А как это получилось, попробуйте разобраться самостоятельно. Дополнительная информация будет позже. Если кто захочет прорешать определитель до конца, правильный ответ: 18. Для тренировки лучше раскрыть определитель по какому-нибудь другому столбцу или другой строке.

Потренироваться, раскрыть, провести расчёты – это очень хорошо и полезно. Но сколько времени вы потратите на большой определитель? Нельзя ли как-нибудь быстрее и надёжнее? Предлагаю ознакомиться с эффективными методами вычисления определителей на втором уроке – Свойства определителя. Понижение порядка определителя .

БУДЬТЕ ВНИМАТЕЛЬНЫ!

Метод Крамера основан на использовании определителей в решении систем линейных уравнений. Это значительно ускоряет процесс решения.

Метод Крамера может быть использован в решении системы стольких линейных уравнений, сколько в каждом уравнении неизвестных. Если определитель системы не равен нулю, то метод Крамера может быть использован в решении, если же равен нулю, то не может. Кроме того, метод Крамера может быть использован в решении систем линейных уравнений, имеющих единственное решение.

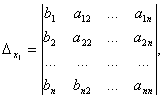
Определение . Определитель, составленный из коэффициентов при неизвестных, называется определителем системы и обозначается (дельта).

Определители

получаются путём замены коэффициентов при соответствующих неизвестных свободными членами:

;

.

Теорема Крамера . Если определитель системы отличен от нуля, то система линейных уравнений имеет одно единственное решение, причём неизвестное равно отношению определителей. В знаменателе – определитель системы, а в числителе – определитель, полученный из определителя системы путём замены коэффициентов при этом неизвестном свободными членами. Эта теорема имеет место для системы линейных уравнений любого порядка.

Пример 1. Решить систему линейных уравнений:

Согласно теореме Крамера имеем:

Итак, решение системы (2):

онлайн-калькулятором , решающим методом Крамера.

Три случая при решении систем линейных уравнений

Как явствует из теоремы Крамера , при решении системы линейных уравнений могут встретиться три случая:

Первый случай: система линейных уравнений имеет единственное решение

(система совместна и определённа)

Второй случай: система линейных уравнений имеет бесчисленное множество решений

(система совместна и неопределённа)

** ,

т.е. коэффициенты при неизвестных и свободные члены пропорциональны.

Третий случай: система линейных уравнений решений не имеет

(система несовместна)

Итак, система m линейных уравнений с n переменными называется несовместной , если у неё нет ни одного решения, и совместной , если она имеет хотя бы одно решение. Совместная система уравнений, имеющая только одно решение, называется определённой , а более одного – неопределённой .

Примеры решения систем линейных уравнений методом Крамера

Пусть дана система

.

На основании теоремы Крамера

………….
,

где
-

определитель системы. Остальные определители получим, заменяя столбец с коэффициентами соответствующей переменной (неизвестного) свободными членами:

Пример 2.

.

Следовательно, система является определённой. Для нахождения её решения вычисляем определители

По формулам Крамера находим:

Итак, (1; 0; -1) – единственное решение системы.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

Если в системе линейных уравнений в одном или нескольких уравнениях отсутствуют какие-либо переменные, то в определителе соответствующие им элементы равны нулю! Таков следующий пример.

Пример 3. Решить систему линейных уравнений методом Крамера:

.

Решение. Находим определитель системы:

Посмотрите внимательно на систему уравнений и на определитель системы и повторите ответ на вопрос, в каких случаях один или несколько элементов определителя равны нулю. Итак, определитель не равен нулю, следовательно, система является определённой. Для нахождения её решения вычисляем определители при неизвестных

По формулам Крамера находим:

Итак, решение системы - (2; -1; 1).

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

К началу страницы

Продолжаем решать системы методом Крамера вместе

Как уже говорилось, если определитель системы равен нулю, а определители при неизвестных не равны нулю, система несовместна, то есть решений не имеет. Проиллюстрируем следующим примером.

Пример 6. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Определитель системы равен нулю, следовательно, система линейных уравнений либо несовместна и определённа, либо несовместна, то есть не имеет решений. Для уточнения вычисляем определители при неизвестных

Определители при неизвестных не равны нулю, следовательно, система несовместна, то есть не имеет решений.

Для проверки решений систем уравнений 3 Х 3 и 4 Х 4 можно воспользоваться онлайн-калькулятором , решающим методом Крамера.

В задачах на системы линейных уравнений встречаются и такие, где кроме букв, обозначающих переменные, есть ещё и другие буквы. Эти буквы обозначают некоторое число, чаще всего действительное. На практике к таким уравнениям и системам уравнений приводят задачи на поиск общих свойств каких-либо явлений и предметов. То есть, изобрели вы какой-либо новый материал или устройство, а для описания его свойств, общих независимо от величины или количества экземпляра, нужно решить систему линейных уравнений, где вместо некоторых коэффициентов при переменных - буквы. За примерами далеко ходить не надо.

Следующий пример - на аналогичную задачу, только увеличивается количество уравнений, переменных, и букв, обозначающих некоторое действительное число.

Пример 8. Решить систему линейных уравнений методом Крамера:

Решение. Находим определитель системы:

Находим определители при неизвестных

1. Определители второго и третьего порядков и их свойства 1.1. Понятие матрицы и определителя второго порядка

Прямоугольную таблицу из чисел, содержащую произвольное число т

строк и произвольное число и столбцов, называют матрицей. Для обозначения

матрицы используют либо сдвоенные вертикальные черточки, либо круглые

скобки. Например:

28 20 18 28 20 18

Если число строк матрицы совпадает с числом ее столбцов, то матрица

называется квадратной. Числа, входящие в состав матрицы, называют ее

элементами .

Рассмотрим квадратную матрицу, состоящую из четырех элементов:

Определителем второго порядка, соответствующим матрице (3.1),

называется число, равное - и обозначаемое символом

Итак, по определению

Элементы, составляющие матрицу данного определителя, обычно

называют элементами этого определителя.

Справедливо следующее утверждение: для того чтобы определитель

второго порядка был равен нулю, необходимо и достаточно, чтобы

элементы его строк (или соответственно его столбцов) были

пропорциональны .

Для доказательства этого утверждения достаточно заметить, что каждая

из пропорций / = / и / = / эквивалентна равенству = , а последнее равенство в

силу (3.2) эквивалентно обращению в нуль определителя.

1.2. Система двух линейных уравнений с двумя неизвестными

Покажем, как применяются определители второго порядка для

исследования и отыскания решений системы двух линейных уравнений с

двумя неизвестными

(коэффициенты, и свободные члены, считаются при этом

заданными). Напомним, что пара чисел, называется решением системы (3.3),

если подстановка этих чисел на место и в данную систему обращает оба

уравнения (3.3) в тождества.

Умножая первое уравнение системы (3.3) на -, а второе - на - и затем

складывая полученные при этом равенства, получим

Аналогично путем умножения уравнений (3.3) на - и соответственно

Введем следующие обозначения:

= , = , = . (3.6)

С помощью этих обозначений и выражения для определителя второго

порядка уравнения (3.4) и (3.5) могут быть переписаны в виде:

Определитель, составленный из коэффициентов при неизвестных

системы (3.3), принято называть определителем этой системы . Заметим, что

определители и получаются из определителя системы посредством замены

его первого или соответственно второго столбца свободными членами.

Могут представиться два случая: 1) определитель системы отличен от

нуля; 2) этот определитель равен нулю.

Рассмотрим сначала случай 0. Из уравнений (3.7) мы сразу же получаем

формулы для неизвестных, называемые формулами Крамера :

Полученные формулы Крамера (3.8) дают решение системы (3.7) и

потому доказывают единственность решения исходной системы (3.3). В самом

деле, система (3.7) является следствием системы (3.3), поэтому всякое

решение системы (3.3) (в случае, если оно существует!) должно являться

решением и системы (3.7). Итак, пока доказано, что если у исходной системы

(3.3) существует при 0 решение, то это решение однозначно определяется

формулами Крамера (3.8).

Легко убедиться и в существовании решения, т. е. в том. что при 0 два

числа и. определяемые формулами Крамера (3.8). будучи поставлены на

место неизвестных в уравнения (3.3), обращают эти уравнения в тождества.

(Предоставляем читателю самому расписать выражения для определителей,

и, и убедиться в справедливости указанных тождеств.)

Мы приходим к следующему выводу: если определитель системы (3.3)

отличен от нуля, то существует, и притом единственное решение этой

системы, определяемое формулами Крамера (3.8).

Рассмотрим теперь случай, когда определитель системы равен нулю .

Могут представиться два подслучая : а) хотя бы один из определителей или,

отличен от нуля; б) оба определителя и равны нулю. (если определитель и

один из двух определителей и равны нулю, то и другой из указанных двух

определителей равен нулю. В самом деле, пусть, например = 0 = 0, т.е. / = /

и / = /. Тогда из этих пропорций получим, что /= /, т. е. = 0).

В подслучае а) оказывается невозможным хотя бы одно из равенств

(3.7), т. е. система (3.7) не имеет решений, а поэтому не имеет решений и

исходная система (3.3) (следствием которой является система (3.7)).

В подслучае б) исходная система (3.3) имеет бесчисленное множество

решений. В самом деле, из равенств === 0 и из утверждения в конце разд. 1.1

заключаем, что второе уравнение системы (3.3) является следствием первого

и его можно отбросить. Но одно уравнение с двумя неизвестными

имеет бесконечно много решений (хотя бы один из коэффициентов, или

отличен от нуля, и стоящее при нем неизвестное может быть определено из

уравнения (3.9) через произвольно заданное значение другого неизвестного).

Таким образом, если определитель системы (3.3) равен нулю, то

система (3.3) либо вовсе не имеет решений (в случае, если хотя бы один из

определителей или отличен от нуля), либо имеет бесчисленное множество

решений (в случае, когда == 0). В последнем случае два уравнения (3.3)

можно заменить одним и при решении его одно неизвестное задавать

произвольно.

Замечание . В случае, когда свободные члены и равны нулю, линейная

система (3.3) называется однородной . Отметим, что однородная система

всегда имеет так называемое тривиальное решение: = 0, = 0 (эти два числа

обращают оба однородных уравнения в тождества).

Если определитель однородной системы отличен от нуля, то эта

система имеет только тривиальное решение. Если же = 0, то однородная

система имеет бесчисленное множество решений (поскольку для

однородной системы возможность отсутствия решений исключена). Таким

образом, однородная система имеет нетривиальное решение в том и только

в том случае, когда определитель ее равен нулю.

1.3. Определители третьего порядка

Рассмотрим квадратную матрицу, состоящую из девяти элементов

Определителем третьего порядка , соответствующим матрице (3.10), называется число, равное:

и обозначаемое символом

Итак, по определению

Как и в случае определителя второго порядка, элементы матрицы (3.10) будем

называть элементами самого определителя . Кроме того, договоримся

называть диагональ, образованную элементами, и, главной , а диагональ,

образованную элементами, и - побочной .

Для запоминания конструкции слагаемых, входящих в выражение для

определителя (3.11), укажем следующее правило, не требующее большого

напряжения внимания и памяти. Для этого к матрице, из которой составлен

определитель, допишем справа еще раз первый, а затем второй столбец. В

полученной при этом матрице

сплошной чертой соединены три тройки членов, получаемые параллельным

переносом главной диагонали и отвечающие трем слагаемым, входящим в

выражение (3.11) со знаком «плюс»; пунктирной же чертой соединены три

другие тройки членов, получаемые параллельным переносом побочной

диагонали и отвечающие трем слагаемым, входящим в выражение (3.11) со

знаком «минус».

1.4. Свойства определителей

Свойство 1 . Величина определителя не изменится, если строки и

столбцы этого определителя поменять ролями, т.е.

Для доказательства этого свойства достаточно расписать определители,

стоящие в левой и правой частях (3.13), по указанному в разд. 1.3 правилу и

убедиться в равенстве полученных при этом членов.

Свойство 1 устанавливает полную равноправность строк и столбцов. Поэтому

все дальнейшие свойства определителя можно формулировать и для строк, и

для столбцов, а доказывать - или только для строк, или только для столбцов.

Свойство 2 . Перестановка двух строк (или двух столбцов)

определителя равносильна умножению его на число -1.

Доказательство также получается из правила, указанного в предыдущем

Свойство 3. Если определитель имеет две одинаковые строки (или два

одинаковых столбца), то он равен нулю .

Действительно, при перестановке двух одинаковых строк, с одной

стороны, определитель не изменится, а с другой стороны, в силу свойства 2

он изменит знак на противоположный. Таким образом, = -, т.е. 2 = 0 или = 0.

Свойство 4. Умножение всех элементов некоторой строки (или

некоторого столбца) определителя на число равносильно умножению

определителя на это число.

Иными словами, общий множитель всех элементов некоторой строки

(или некоторого столбца) определителя можно выносить за знак этого

определителя.

Например,

Для доказательства этого свойства достаточно заметить, что

определитель выражается в виде суммы (3.12), каждый член которой

содержит один и только один, элемент из каждой строки и один и только

один элемент из каждого столбца.

Свойство 5. Если все элементы некоторой строки (или некоторого

столбца) определителя равны нулю, то и сам определитель равен нулю.

Это свойство вытекает из предыдущего (при = 0).

Свойство 6. Если элементы двух строк (или двух столбцов)

определителя пропорциональны, то определитель равен нулю.

В самом деле, в силу свойства 4 множитель пропорциональности можно

вынести за знак определителя, после чего остается определитель с двумя

одинаковыми строками, равный нулю согласно свойству 3.

Свойство 7. Если каждый элемент п-й строки (или п-го столбца)

определителя представляет собой сумму двух слагаемых, то определитель

может быть представлен в виде суммы двух определителей, первый из

которых имеет в п-й строке (или в п-м столбце) первые из упомянутых

слагаемых и те же элементы, что и исходный определитель, в остальных

строках (столбцах), а второй определитель имеет в п-й строке (в п-м

столбце) вторые из упомянутых слагаемых и те же элементы, что и

исходный определитель, в остальных строках (столбцах).

Например,

Для доказательства этого свойства снова достаточно заметить, что

определитель выражается в виде суммы слагаемых, каждое из которых

содержит один и только один элемент из каждой строки и один и только один

элемент из каждого столбца.

Свойство 8. Если к элементам некоторой строки (или некоторого

столбца) определителя прибавить соответствующие элементы другой

строки (другого столбца), умноженные на произвольный множитель, то

величина определителя не изменится .

Действительно, полученный в результате указанного прибавления

определитель можно (в силу свойства 7) разбить на сумму двух

определителей, первый из которых совпадает с исходным, а второй равен

нулю вследствие пропорциональности элементов двух строк (или столбцов) и

свойства 6.

1.5. Алгебраические дополнения и миноры

Соберем в выражении (3.12) для определителя члены, содержащие

какой-нибудь один элемент этого определителя, и вынесем указанный элемент

за скобки; величина, остающаяся при этом в скобках, называется

алгебраическим дополнением указанного элемента.

Алгебраическое дополнение данного элемента мы будем обозначать

прописной латинской буквой того же наименования, что и данный элемент, и

снабжать тем же номером, который имеет данный элемент. Например,

алгебраическое дополнение элемента будем обозначать через алгебраическое

дополнение элемента - через и т. д.

Непосредственно из выражения для определителя (3.12) и из того, что

каждое слагаемое в правой части (3.12) содержит один и только один элемент

из каждой строки (из каждого столбца), вытекают следующие равенства:

Эти равенства выражают следующее свойство определителя:

определитель равен сумме произведений элементов какой-либо строки

(какого-либо столбца) на соответствующие алгебраические дополнения

элементов этой строки (этого столбца).

Равенства (3.14) принято называть разложением определителя по

элементам соответственно первой, второй или третьей строки, а равенства

(3.15) - разложением определителя по элементам соответственно первого,

второго или третьего столбца.

Введем теперь важное понятие минора данного элемента определителя

Минором данного элемента определителя n-го порядка (в нашем случае n = 3)

называется определитель (n-1)-го порядка, получаемый из данного

определителя путем вычеркивания той строки и того столбца, на пересечении

которых стоит данный элемент.

Алгебраическое дополнение любого элемента определителя равняется

минору этого элемента, взятому со таком «плюс», если сумма номеров

строки и столбца, на пересечении которых стоит данный элемент, есть

число четное, и со знаком «минус» - в противном случае.

Таким образом, соответствующие алгебраическое дополнение и минор

могут отличаться только знаком.

Следующая таблица дает наглядное представление о том, каким знаком

связаны соответствующие алгебраическое дополнение и минор:

Установленное правило позволяет в формулах (3.14) и (3.15) разложения

определителя по элементам строк и столбцов всюду вместо алгебраических

дополнений писать соответствующие миноры (с нужным знаком).

Так, например, первая из формул (3.14), дающая разложение

определителя по элементам первой строки, принимает вид

В заключение установим следующее фундаментальное свойство

определителя.

Свойство 9. Сумма произведений элементов какого-либо столбца

определителя на соответствующие алгебраические дополнения элементов

этого {другого) столбца равна величине этого определителя (равна нулю).

Конечно, аналогичное свойство справедливо и в применении к строкам

определителя. Случай, когда алгебраические дополнения и элементы

отвечают одному и тому же столбцу, уже рассмотрен выше. Остается доказать,

что сумма произведений элементов какого-либо столбца на соответствующие

алгебраические дополнения элементов другого столбца равна нулю.

Докажем, например, что сумма произведений элементов первого или

третьего столбца равна нулю.

Будем исходить из третьей формулы (3.15), дающей разложение

определителя по элементам третьего столбца:

Так как алгебраические дополнения, и элементов третьего столбца не

зависят от самих элементов, и этого столбца, то в равенстве (3.17) числа, и

можно заменить произвольными числами, и, сохраняя при этом в левой

части (3.17) первые два столбца определителя, а в правой части - величины,

и алгебраических дополнений.

Таким образом, при любых , и справедливо равенство:

Беря теперь в равенстве (3.18) в качестве, и сначала элементы, и

первого столбца, а затем элементы, и второго столбца и учитывая, что

определитель с двумя совпадающими столбцами в силу свойства 3 равен

нулю, мы придем к следующим равенствам:

Тем самым доказано, что сумма произведений элементов первого или

второго столбца на соответствующие алгебраические дополнения элементов

третьего столбца равна нулю: Аналогично доказываются равенства:

и соответствующие равенства, относящиеся не к столбцам, а к строкам:

2. Системы линейных уравнений с тремя неизвестными 2.1. Системы трех линейных уравнений с тремя неизвестными с

определителем, отличным от нуля.

В качестве приложения изложенной выше теории рассмотрим систему

трех линейных уравнений с тремя неизвестными:

(коэффициенты, , и свободные члены, считаются заданными).

Тройка чисел, называется решением системы (3.19), если подстановка этих

чисел на место, в систему (3.19) обращает все три уравнения (3.19) в

тождества.

Фундаментальную роль в дальнейшем будут играть следующие четыре

определителя:

Определитель принято называть определителем системы (3.19) (он

составлен из коэффициентов при неизвестных). Определители, и

получаются из определителя системы посредством замены свободными

членами элементов соответственно первого, второго и третьего столбцов.

Для исключения из системы (3.19) неизвестных и умножим уравнения

(3.19) соответственно на алгебраические дополнения, элементов первого

столбца определителя системы, и после этого сложим полученные при этом

уравнения. В результате получим:

Учитывая, что сумма произведений элементов данного столбца

определителя на соответствующие алгебраические дополнения элементов

этого (другого) столбца равна определителю (нулю) (см. свойство 9),

0, ++= 0.

Кроме того, посредством разложения определителя по элементам первого столбца получается формула:

С помощью формул (3.21) и (3.22) равенство (3.20) перепишется в

следующем (не содержащем неизвестных и) виде:

Совершенно аналогично выводятся из системы (3.19) равенства = и

Таким образом, мы установили, что система уравнений = , = , =

является следствием исходной системы (3.19).

В дальнейшем мы отдельно рассмотрим два случая:

1) когда определитель системы отличен от нуля ,

2) когда этот определитель равен нулю .

Итак, пусть 0. Тогда из системы (3.23) мы сразу получаем формулы для неизвестных, называемые формулами Крамера :

Полученные нами формулы Крамера дают решение системы (3.23) и

потому доказывают единственность решения исходной системы (3.19), ибо

система (3.23) является следствием системы (3.19), и всякое решение системы

(3.19) обязано быть решением и системы (3.23).

Итак, мы доказали, что если у исходной системы (3.19) существует при

0 решение, то это решение однозначно определяется формулами Крамера

Чтобы доказать, что решение в самом деле существует, мы должны

подставить в исходную систему (3.19) на место х, у и z их значения,

определяемые формулами Крамера (3.24), и убедиться в том, что все три

уравнения (3.19) обращаются при этом в тождества. Убедимся, например, что

первое уравнение (3.19) обращается в тождество при подстановке значений х,

у и z, определяемых формулами Крамера (3.24). Учитывая, что

получим, подставив в левую часть первого из уравнений (2.19) значения, и,

определяемые формулами Крамера:

Группируя внутри фигурной скобки члены относительно A, А2 и Л3,

получим, что:

В силу свойства 9 в последнем равенстве обе квадратные скобки равны

нулю, а круглая скобка равна определителю. Таким образом, мы получим ++

И обращение в тождество первого уравнения системы (3.19) установлено.

Аналогично устанавливается обращение в тождество второго и третьего

уравнений (3.19).

Мы приходим к следующему выводу: если определитель системы (3.19)

отличен от нуля, то существует, и притом единственное, решение этой

системы, определяемое формулами Крамера (3.24).

2.2. Однородная система двух линейных уравнений с тремя неизвестными

В этом и в разделе мы разовьем аппарат, необходимый для рассмотрения неоднородной системы (3.19) с определителем, равным нулю. Сначала рассмотрим однородную систему двух линейных уравнений с тремя неизвестными:

Если все три определителя второго порядка, которые можно

составить из матрицы

равны нулю , то в силу утверждения из разд. 1.1 коэффициенты первого из

уравнений (3.25) пропорциональны соответствующим коэффициентам

второго из этих уравнений. Стало быть, в этом случае второе уравнение (3.25)

является следствием первого, и его можно отбросить. Но одно уравнение с

тремя неизвестными ++= 0, естественно, имеет бесчисленное множество

решений (двум неизвестным можно предписывать произвольные значения, а

третье неизвестное определять из уравнения).

Рассмотрим теперь систему (3.25) для случая, когда хотя бы один из

определителей второго порядка, составленных из матрицы (3.26), отличен

от нуля. Не ограничивая общности, будем считать, что отличен от нуля

определитель

0 Тогда мы можем переписать систему (3.25) в виде

и утверждать, что для каждого z существует единственное решение этой

системы, определяемое формулами Крамера (см. разд. 1.2, формулы (3.8)):

третьей строки определителя:

В силу результатов разд. 1.5 о связи алгебраических дополнений и

миноров можно записать

Основываясь на (3.29), мы можем переписать формулы (3.28) в виде

Для того чтобы получить решение в виде, симметричном

относительно всех неизвестных х, у, и z, положим (отметим, что в силу (3.27)

определитель отличен от нуля). Поскольку z может принимать любые

значения, то и новая переменная t может принимать любые значения .

Мы приходим к выводу, что в случае, когда определитель (3.27) отличен от нуля, однородная система (3.25) имеет бесчисленное множество решений, определяемых формулами

в которых t принимает какие угодно значения, а алгебраические

дополнения, и определяются формулами (3.29).

2.3. Однородная система трех линейных уравнений с тремя неизвестными

Рассмотрим теперь однородную систему трех уравнений с тремя

неизвестными:

Очевидно, что эта система всегда имеет так называемое тривиальное

решение: х = 0, у = 0, z = 0.

В случае, когда определитель системы, это тривиальное решение

является единственным (в силу разд. 2.1).

Докажем, что в случае, когда определитель равен нулю, однородная

система (3.32) имеет бесчисленное множество решений.

Если все определители второго порядка, которые можно составить из

равны нулю, то в силу утверждения из разд. 1.1 соответствующие

коэффициенты всех трех уравнений (3.32) пропорциональны. Но тогда второе

и третье уравнения (3.32) являются следствиями первого и могут быть

отброшены, а одно уравнение ++= 0, как уже отмечалось в разд. 2.2, имеет

бесчисленное множество решений.

Остается рассмотреть случай, когда хотя бы один минор матрицы (3.33)

отличен от нуля. Так как порядок следования уравнений и неизвестных

находится в нашем распоряжении, то, не ограничивая общности, мы можем

разд. 2.2, система первых двух уравнений (3.32) имеет бесчисленное

множество решений, определяемых формулами (3.31) (при любом t).

Остается доказать, что х, у, z, определяемые формулами (3.31) (при

любом t, обращают в тождество и третье уравнение (3.32). Подставляя в

левую часть третьего уравнения (3.32) х, у и z, определяемые формулами

(3.31), получим

Мы воспользовались тем, что в силу свойства 9 выражение в круглых

скобках равно определителю системы (3.32). Но определитель по условию

равен нулю, и поэтому при любом t мы получим ++= 0.

Итак, доказано, что однородная система (3.32) с определителем А.

равным нулю, имеет бесчисленное множество решений . Если отличен от нуля

минор (3.27), то эти решения определяются формулами (3.31) при

произвольно взятом t.

Полученный результат можно сформулировать еще и так: однородная

система (3.32) имеет нетривиальное решение в том и только в том случае,

когда определитель ее равен нулю .

2.4. Неоднородная система трех линейных уравнений с тремя

неизвестными с определителем, равным нулю.

Теперь мы располагаем аппаратом для рассмотрения неоднородной

системы (3.19) с определителем, равным нулю. Могут представиться два

случая: а) хотя бы один из определителей, или - отличен от нуля; б) все три

определителя, и равны нулю.

В случае а) оказывается невозможным хотя бы одно из равенств (3.23),

т. е. система (3.23) не имеет решений, а поэтому не имеет решений и исходная

система (3.19) (следствием которой является система (3.23)).

Переходим к рассмотрению случая б), когда все четыре определителя , ,

и равны нулю. Начнем с примера, показывающего, что и в этом случае

система может не иметь ни одного решения. Рассмотрим систему:

Ясно, что эта система не имеет решений. В самом деле, если бы

решение, существовало, то из первых двух уравнений мы получили бы, а

отсюда, умножая первое равенство на 2, получили бы, что 2 = 3. Далее,

очевидно, что все четыре определителя , , и равны нулю. Действительно,

определитель системы

имеет три одинаковых столбца , определители, и получаются путем замены

одного из этих столбцов свободными членами и, стало быть, имеют по два

одинаковых столбца. В силу свойства 3 все эти определители равны нулю.

Докажем теперь, что если система (3.19) с определителем, равным

нулю, имеет хотя бы одно решение, то она имеет бесчисленное множество

различных решений.

Предположим, что указанная система имеет решение, . Тогда

справедливы тождества

Вычитая почленно из уравнений (3.19) тождества (3.34), получим

систему уравнений

эквивалентную системе (3.19). Но система (3.35) является однородной

системой трех линейных уравнений относительно трех неизвестных, и с

определителем, равным нулю. Согласно разд. 2.3 последняя система (а стало

быть, и система (3.19)) имеет бесчисленное множество решений. Например, в

случае, когда отличен от нуля минор (3.27), мы с помощью формул (3.31)

получим следующее бесконечное множество решений системы (3.19):

(t принимает любые значения).

Сформулированное утверждение доказано, и мы можем сделать

следующее заключение: если = = = = 0, то неоднородная система уравнений

(3.19) либо совсем не имеет решений, либо имеет их бесконечное множество.

3. Понятие об определителях любого порядка и о линейных

системах с любым числом неизвестных Установленное нами свойство разложения определителя третьего

порядка до элементам любой (например, первой) строки может быть

положено в основу последовательного введения по индукции определителя

четвертого, пятого и всех последующих порядков.

Предположим, что нами уже введено понятие определителя порядка

(n-1), и рассмотрим произвольную квадратную матрицу состоящую из

элементов

Назовем минором любого элемента матрицы (3.36) уже введенный нами

определитель порядка (n-1), отвечающий матрице (3.36), у которой удалены i-

я строка и j-й столбец. Договоримся обозначать минор элемента символом.

Например, минор любого элемента первой строки матрицы (3.36)

является следующим определителем порядка (n-1):

Назовем определителем порядка n, отвечающим матрице (3.36), число,

равное сумме

и обозначаемое символом

= Заметим, что при n = 3 разложение (3.37) совпадает с разложением

(3.16) определителя третьего порядка по первой строке.

Рассмотрим теперь неоднородную систему n уравнений с n неизвестными:

Определитель порядка n, составленный из коэффициентов при

неизвестных системы (3.39) и совпадающий с определителем из равенства

(3.38), называется определителем этой системы При любом j, равном 1, 2, ...,

n, обозначим символом определитель порядка n, полученный из определителя

системы путем замены его j-го столбца столбцом свободных членов, ..., .

В полной аналогии со случаем n = 3 оказывается справедлив

следующий результат: если определитель неоднородной системы (3.39)

отличен от нуля, то эта система имеет единственное решение,

определяемое формулами Крамера :

хотя бы один из определителей, ..., отличен от нуля, то система (3.39) не

имеет решений .

В случае же, если n > 2 и все определители, ..., равны нулю, система

(3.39) может также не иметь решений, но если она имеет хотя бы одно

решение, то она имеет их бесчисленное множество.

4. Отыскание решения линейной системы методом Гаусса Рассмотрим неоднородную систему (3.39), в которой мы теперь для

сокращения записи переобозначим свободные члены, ..., используя для них

обозначение при i = 1, 2 ..., n. Изложим один из самых простых методов

решения этой системы, заключающийся в последовательном исключении

неизвестных и называемый методом Гаусса .

Выберем из коэффициентов при неизвестных коэффициент, отличный

от нуля, и назовем его ведущим. Не ограничивая общности, будем считать,

что таким коэффициентом является (иначе мы могли бы поменять порядок

следования неизвестных и уравнений).

Поделив все члены первою уравнения (3.39) на, получим первое приведенное уравнение

в котором при j = 1, 2, ..., (n+1).

Напомним, что, и, в частности, .

Для исключения неизвестного вычтем из i-го уравнения системы (3.39)

(i = 2, 3 ..., n)

умноженное на приведенное уравнение (3.40).

В результате получим для любого i = 2, 3, ..., n уравнение

в котором

при j = 2, 3, ..., (n+1).

Таким образом, мы получаем первую укороченную систему:

коэффициенты которой определяются по формулам (3.41).

В системе (3.42) находим отличный от нуля ведущий коэффициент.

Пусть это будет. Тогда, поделив первое уравнение (3.42) на этот

коэффициент, мы получим второе приведенное уравнение и, исключив с

помощью этого уравнения по описанной выше схеме неизвестное, придем ко

второй укороченной системе, не содержащей и.

Продолжая рассуждения по этой схеме, называемой прямым ходом

метода Гаусса , мы либо завершим ее реализацию, дойдя до линейного

уравнения, содержащего только одно неизвестное, либо не сможем завершить

ее реализацию (вследствие того, что исходная система (3.39) не имеет

решений). В случае, если исходная система (3.39) имеет решения, мы получим

цепочку приведенных уравнений

из которой обратным xодом метода Гаусса последовательно находятся

неизвестные

Подчеркнем, что все операции при обратном ходе метода Гаусса (1.43)

выполняются без деления,

В качестве примера рассмотрим неоднородную систему трех уравнений

с тремя неизвестными

Конечно, можно убедиться в том, что определитель системы (3.44)

отличен от нуля, и найти, и по формулам Крамера, но мы применим метод

Поделив первое уравнение системы (3.44) на 2, получим первое

приведенное уравнение:

Вычитая из второго уравнения системы (3.44) приведенное уравнение

(3.45), умноженное на 3, и вычитая из третьего уравнения системы (3.44)

приведенное уравнение (3.45), умноженное на 4, мы получим укороченную

систему двух уравнений с двумя неизвестными:

Поделив первое уравнение (3.46) на, получим второе приведенное

уравнение:

Вычитая из второго уравнения (3.46) приведенное уравнение (3.47),

умноженное на 8, получим уравнение:

которое после сокращения на дает = 3.

Подставляя это значение во второе приведенное уравнение (3.47), получим,

что = -2. Наконец, подставляя найденные значения = -2 и = 3 в первое

приведенное уравнение (3.45), получим, что = 1.

ЛИТЕРАТУРА 1. Ильин В.А., Куркина А.В. – «Высшая математика», М.:ТК Велби, изд-во Проспект,